Simpson's Paradox
Simpson's paradox is a statistical phenomenon that occurs when a pattern across groups of data disappears when those groups are combined.
A famous example of this is UC Berkeley's admission rates for its 1973 class. The school discovered that it had admitted 44% of male applicants and 35% of female applicants.
On the surface, this looked like a considerable gender bias, but when they examined the data more closely, they discovered that women tended to apply to departments with more competitive rates of admission, while men tended to apply to less competitive departments.
Not only that, but because 6 departments were biased towards women, while only 4 departments were biased towards men, that year's class skewed in favor of accepting women, even though they had a lower overall acceptance rate.
This idea can be tricky to grok at first, so here's another example:
In baseball, player A can have a lower batting average than player B two years in a row. But if there is a discrepancy between the number of at bats they have, player A can have a higher batting average over the course of both years.
Here's how this played out for Derek Jeter and David Justice in the 1995-96 seasons:
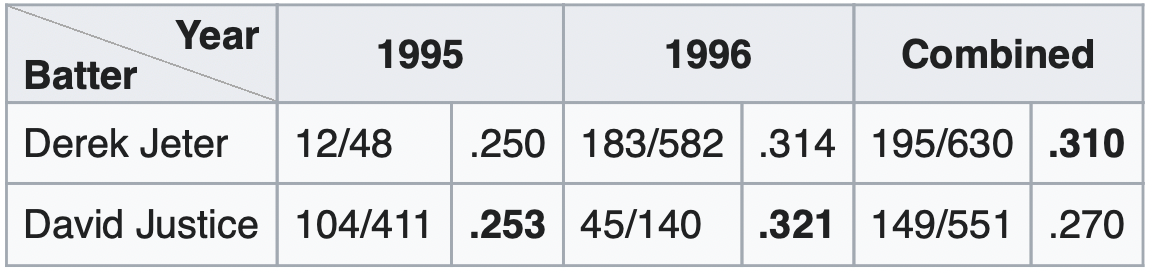
Justice had a higher batting average both years, but Jeter had more at bats, so when the data are combined, Justice's lead disappears.
The common thread across both these examples is that there are hidden variables at play. The competitiveness of each of UC Berkeley's departments and the number of at bats are both concealed by the summarized data.
Simpson's paradox is an important reminder that our intuition is important when analyzing something.
Our intuition helps us figure out which questions to ask, and knowing what to ask is half the battle.
